Mathdocs

Github

Goals

The goal of this project was:

1. To build a tool for myself to support my educational objectives that I could use regularly
2. To test out an idea I had about mathematics knowledge being structured like code, with inheritance and relationships, rather than a linear process of building towards a big proof or result
3. To gain familiarity with Django (this was my first time working with Django)
4. To expose myself to a CSS framework other than Bootstrap

Overview

This project is a Django app that allows me to document mathematics knowledge in a way similar to how I document code. It emphasizes inheritance between mathematical objects and use relationships between theorems and objects in the following ways:

Concepts

Mathematical concepts are divided into four categories:

1. Mathematical objects
2. Mathematical properties
3. Axioms
4. Theorems

Mathematical Objects

Most of the ideas we worked with in my math classes were objects: groups, sets, elements in sets, subsets with particular properties, etc.

That said, we rarely made an explicit note of the fact that objects had particular properties or were derived from other objects, so I wanted to emphasize that in this organizational scheme.

Mathematical Properties

Often, we had several objects that weren’t necessarily related to one another, but which shared particular properties, so I have properties as a separate concept. Properties can belong to objects, and are referenced in theorems.

Theorems

Theorems are simply statements about objects, their behaviors, natures, properties, and relationships. Theorems come in several varieties–corollaries, lemmas, and plain old theorems–but they are all essentially the same: the are statements that have proofs. Contrast that with axioms.

Axioms

Axioms are statements that cannot be (or don’t need to be) proved. I included them as distinct from theorems because all I needed to know about them was their statement and where they are used, not the steps for proving them.

Organization

Objects can have parent and children objects derived from one another, and they can also contain other classes of objects. For example, groups are parents of subgroups, and contain sets and operations. Sets contain elements, but elements are not derived from sets (though sets can be elements).

The way the app is organized, whenever you are viewing a particular mathematical object, you will see how it fits into the bigger picture: what is it derived from, what is derived from it, what theorems is it used in, and what properties does it have. This gives a much more holistic picture of the field of mathematics that we’re in that the standard textbook presentation, which is linear and does not explicitly refer to the relationships being explored.

Skills used and acquired

• The project forced me to formalize the way I understand mathematics, which in itself was really useful.
• I learned Django roughly, its assumptions and processes, and how to move around in a Python-based web framework (in contrast to my prior experience with JS and C#).
• I improved my understanding and utilization of database models, migrations, and interactions with the application layer.
• I learned a new CSS framework, FomanticUI, which was fun, quite different from Bootstrap, and much sleeker-looking, which I appreciated.
• Improved general familiarity with Python.

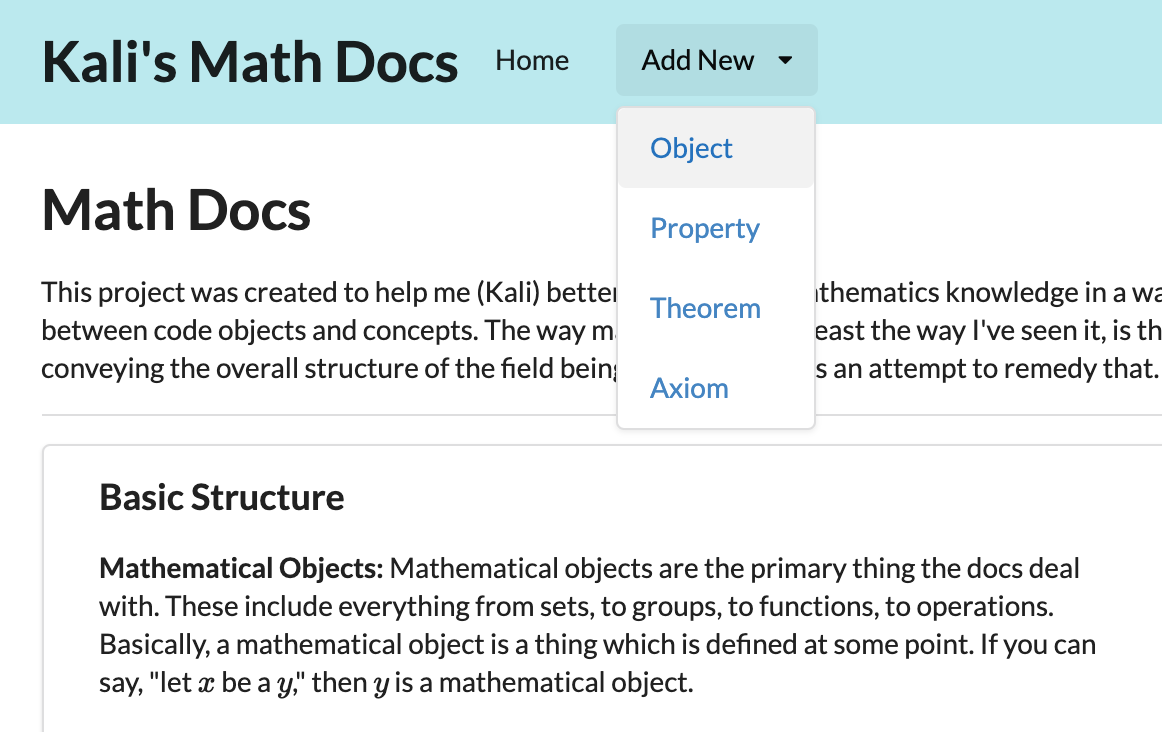
Pictures

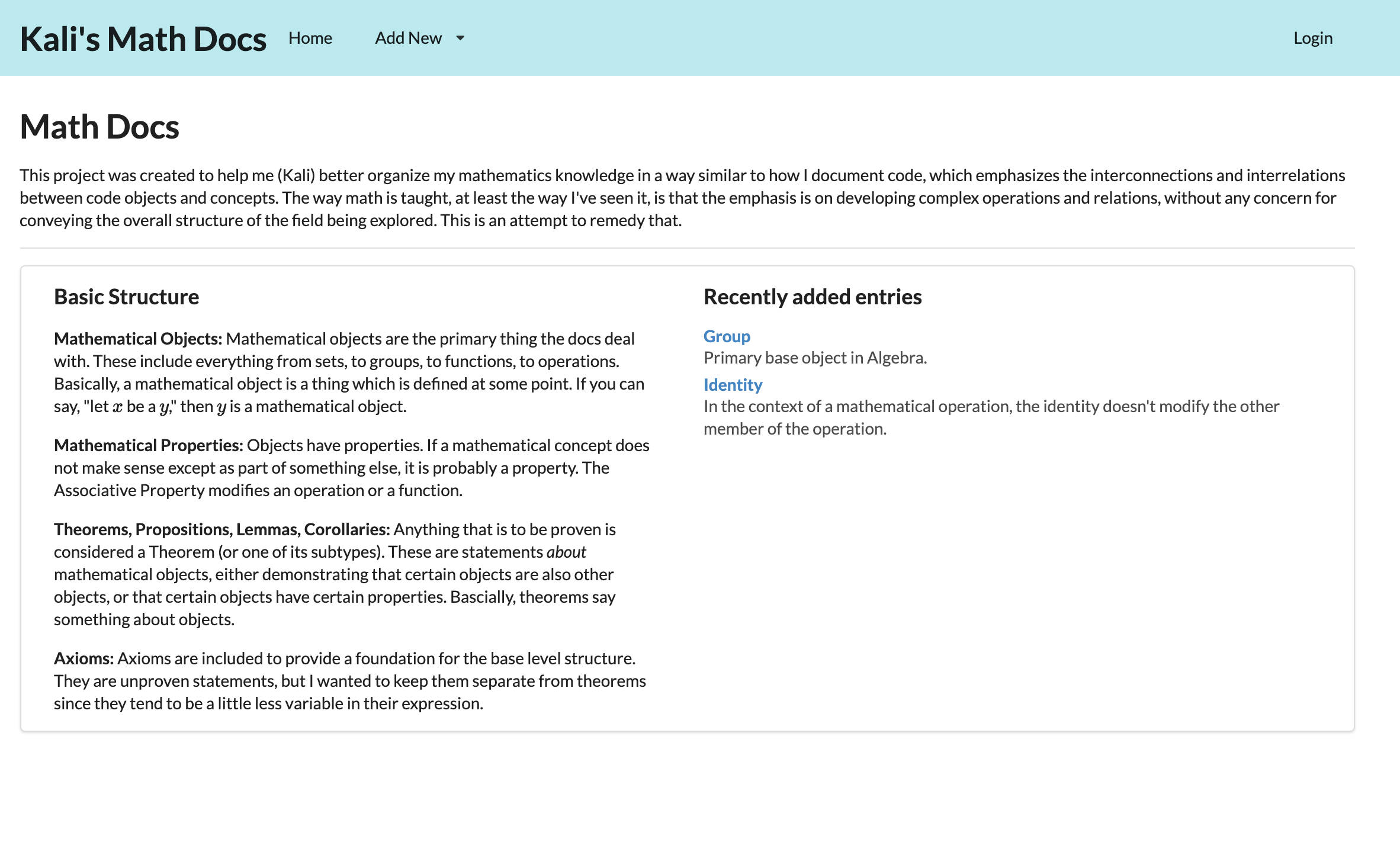
Lessons learned

• There are already better ways to do this, honestly. Personal wikis exist and can be easily utilized to create a math documentation in the model I envisioned. At first, this was discouraging, and in fact led to a long stall on the project. However, I eventually come to see the project as a learning opportunity for its own sake, regardless of whether or not I made a tool I’d use in favor of a better one.
• I learned that I kind of like having to build everything from the ground up. Django makes a lot of (very helpful) assumptions, but for me, this can often hinder an understanding of what’s happening or why things don’t work. If I have to build something from scratch, I understand all the errors because there are no assumptions I didn’t put in place myself.
• That said, once I did start to understand Django, it was really nice to let it handle basic processes that follow common patterns (like basic user authentication, which I set up in less than an hour).

Future directions for the projects

The next time I take on learning a new area of mathematics, especially if self-taught, I will use this tool to keep my notes and see if it helps. In that case, I may publish it online so that I can access it from anywhere and have a secure back-up of all the information.

For now, though, I will probably leave it as a personal tool, and just run it on my personal computer when I need it, unless people make requests for it. I’d also like to expand some of the study support tools. Right now, the only one is that you can enter theorem proofs in steps that can be hidden and shown incrementally, so you can test yourself on your understanding of the proof and self-generate it.